\(\Lambda\)粒子¶
在这一章我们一起来重建\(\Lambda\),那在开始之前,你需要在PDG上仔细地研究一下这个粒子。它的质量大概是 \(1.115GeV\),而寿命 \(\tau_{\Lambda}\approx2.617\times10^{−10}s\),比 \(K_s\)的寿命大了3倍,我们同样可以利用这一显著的特征来去除本底。再看它的衰变模式,我们发现\(\Lambda\rightarrow p^+\pi^-\)的分支比大概是\(64.1\%\),因此我们可以在 \(p^+\pi^-\)衰变道来寻找\(\Lambda\)粒子。
1-Ntuple Maker¶
\(p^+\pi^-\)的寻找和\(\pi^+\pi^-\)一样,都是通过带电粒子的track来匹配和重建的。两者唯一的区别在于two tracks fit部分。
对于\(\pi^+\pi^-\),由于两者质量相同,无论我们认为第一个 \(\pi\) 的track是track1还是track2其实都一样。
但是对于\(p^+\pi^-\),\(p^+\)的质量是 \(0.938GeV\),\(\pi^-\)的质量是 \(0.139GeV\),两者相差了9倍,在物理上我们可以证明:在实验室系中,\(p^+\)的动量大于 \(\pi^-\)。
这里给出证明。
在\(\Lambda\)质心系,\(\Lambda\)的动量为0,根据动量守恒定律,\(|\vec{p_p^*}|=|\vec{p_\pi^*}|=p^*\),能量 \(E_p^*=\sqrt{p{^*}^2+m_p^2}\),\(E_\pi^*=\sqrt{p{^*}^2+m_\pi^2}\),由于 \(m_p > m_\pi\),所以 \(E_p^* > E_\pi^*\)。
取\(p\)的动量在质心系与z轴夹角为 \(\theta\),则\(p\)的纵向分量 \(p_{p,z}^* = p^*\cos\theta\),\(\pi\)的纵向分量 \(p_{\pi,z}^* = -p^*\cos\theta\)。两者横向分量相等,\(p_T^* = p^*\sin\theta\)。
对\(\Lambda\)做沿着+z方向的boost,由洛伦兹变换
\[\begin{pmatrix} E \\ p_x \\ p_y \\ p_z \end{pmatrix} = \begin{pmatrix} \gamma & 0 & 0 & \gamma\beta \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \gamma\beta & 0 & 0 & \gamma \end{pmatrix} \begin{pmatrix} E^* \\ p_x^* \\ p_y^* \\ p_z^* \end{pmatrix}\]可得 \(p_{p,z}=\gamma(\beta E_p^*+p_{p,z}^*)=\gamma(\beta E_p^*+p^*\cos\theta)\),\(p_{\pi,z}=\gamma(\beta E_\pi^*+p_{\pi,z}^*)=\gamma(\beta E_\pi^*-p^*\cos\theta)\),而横向分量在boost下不变,\(p_T=p_T^*=p^*\sin\theta\)。
为了简便,我们假设 \(\theta=0\)。
则差值 \(\Delta p^2 = p_p^2-p_\pi^2 = p_{p,z}^2-p_{\pi,z}^2=\gamma^2(E_p^*+E_\pi^2)[2\beta p^*+\beta^2(E_p^*-E_\pi^*)]>0\)。得证。
因此我们只需要修改two tracks fit部分的代码。
2-产生multilep.root文件¶
这一部分和 \(K_s\)类似,我们要交crab作业来产生大量multilep.root。
3-myntuple分析root文件¶
这一部分和 \(K_s\)类似,下面仅列出我的myntuple.C的筛选条件部分作为参考。
这里要说明一下,我当时在.cc中限制了\(p\)为正电荷,\(\pi\)为负电荷,因此我下面重建的结果都是\(\Lambda\)正粒子。
最终得到的\(\Lambda\)粒子长成这样
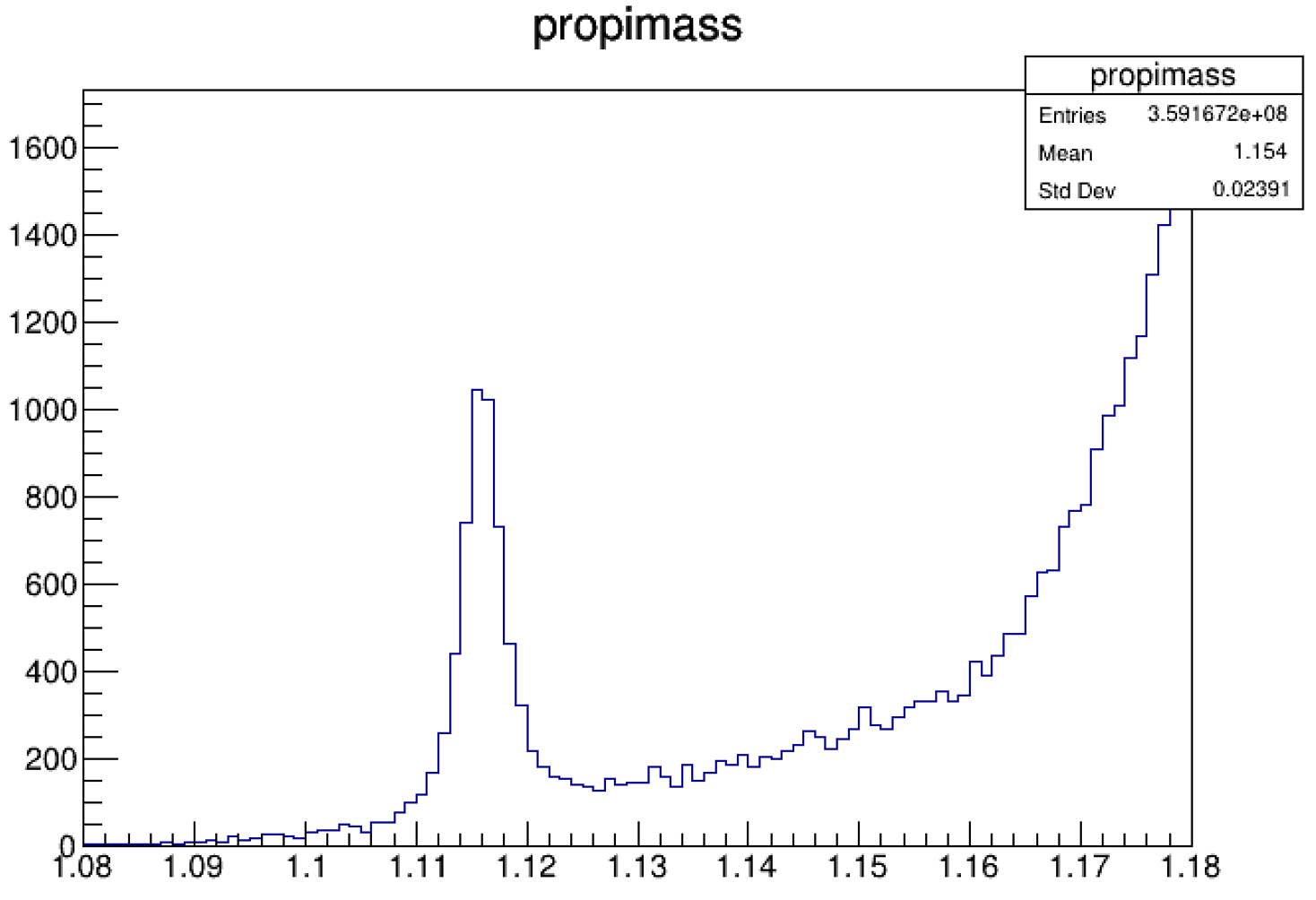
看到这个峰是不是有点激动?你会感觉\(\Lambda\)粒子比 \(K_s\)更容易找到,主要是有以下两点原因:
- 在two tracks fit中,将大动量的track赋给了proton,小动量的track赋给了pion,相当于手动排除了另一种可能性,大大减少了错误的重建(本底)。
- \(p + \pi\)的质量阈值大概在 \(1.07GeV\),而\(\Lambda\)粒子的质量大概是 \(1.115GeV\),略高于阈值,而本底在阈值附近会因为相空间受限而迅速减少,因此你看到的\(\Lambda\)和\(K_s\)相比非常干净。
4-Fit¶
找到 \(\Lambda\) 粒子之后你同样需要对它做拟合。由于 \(\Lambda\) 的宽度很窄,所以这里采用高斯函数+水晶球函数拟合信号,二阶切比雪夫多项式拟合本底。下面仅列出我的fitLamda.C作为参考。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 | |
这里有几点小trick:
- 你会发现上面的直方图的事例非常多,我们需要考虑是采用Unbinned fit还是Binned fit。Unbinned fit是对每一个数据点进行拟合,Binned fit是对每个bin进行拟合,他们之间有几个数量级的差别。如果\(\Lambda\)和\(K_s\)一样采用Unbinned fit,那拟合的速度会非常慢,效率极低因此这里选择做Binned fit。
- 细心的你会发现\(\Lambda\)的拟合程序有这么一句话:
gROOT->SetBatch(kTRUE);,这个命令是要求程序拟合完之后不产生图直接结束运行的,图会保存在相应的pdf里。像lxplus和lpc这样的国外远程服务器,产生图的速度会非常慢,效率极低。我们可以直接把pdf拷贝到本地来查看,速度翻番!
拟合结果已经展示在图上。注意这里仅重建了\(\Lambda\)正粒子。同样,在这里看到的信号“宽度”其实并不是\(\Lambda\)真正的宽度,它是由探测器的resolution(分辨率)所决定的。
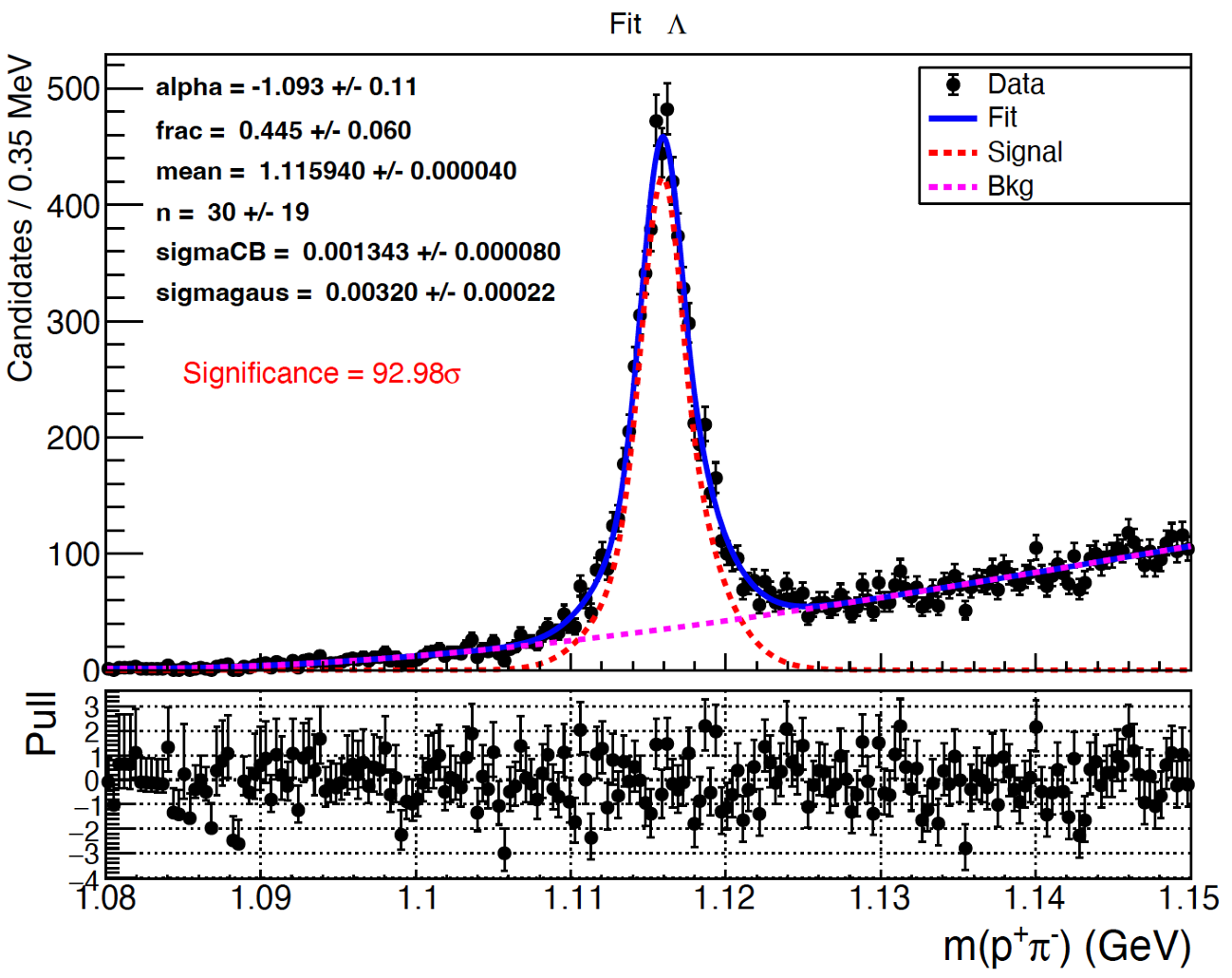
恭喜你又成功地完整地打通了\(\Lambda\)这一关!凭借自己的努力找到粒子是不是非常有成就感?将抽象的粒子具象化是不是感觉还挺有趣的?但是故事还没有结束......下一章我们会继续挑战重建\(\Omega^-\)粒子!