\(K_s\)粒子¶
在这一章我们一起来重建\(K_s\),那在开始之前,你需要在PDG上仔细地研究一下这个粒子。它的质量大概是 \(0.497GeV\),而寿命 \(\tau_{K_s}\approx8.954\times10^{−11}s\)比一般粒子要长,这是它区别于其他粒子的一个非常显著的特征。再看它的衰变模式,我们发现\(K_s\rightarrow \pi^+\pi^-\)的分支比大概是\(69.2\%\),因此我们可以在 \(\pi^+\pi^-\)衰变道来寻找 \(K_s\)粒子。
1-Ntuple Maker¶
由于CMS探测器可以记录带电强子的track,我们是通过对track的寻找和匹配来重建 \(\pi^+\pi^-\)的。
1.1-track数据集¶
对于track的寻找,我们用的是"packedPFCandidates"数据集。可以用下面的方式查看这个数据集的tag。
参照朱峰学长的Multilep learning note中的教程,我们可以把.h文件和.cc文件进行以下修改。
类似的,这里的trackToken_是一个成员变量,它保存了一个Token。这个Token表示模块需要pat::PackedCandidate类型的对象,数据来源是一个名为“packedPFCandidates”的数据集(由edm::InputTag指定)。这个数据集名称是在数据处理链中定义的,用于标识数据源。
1.2-for循环起始¶
下面就是最关键的对两个track的循环部分。
1.3-two tracks fit¶
在输出变量之前,我们需要仔细思考自己需要用到哪些变量。\(K_s\)粒子的一个非常重要的特征是寿命比较长,我们要抓住这个特点筛选掉干扰我们寻找 \(K_s\)粒子的本底,所以 \(c\tau\)是一个必须要输出的变量,关于 \(c\tau\)的定义在Multilep learning note中的10-mass constraint结尾可以找到。另外,我们是通过两个track来重建\(K_s\)的,因此必须保证两个track是从同一个顶点出来的,而对应的物理量是vertex ChiSquared Probability,这个值越接近1就表示两个track从同一个顶点出来的可能性越大,如果没有Vertex Probability,我们重建出来的 \(\pi^+\pi^-\)质量绝大部分都是本底(垃圾)。
试着把下面这些变量在tree里面都存储下来。
请记住在完成.h和.cc文件的编写之后需要编译。
2-产生multilep.root文件¶
2.1-cmsRun本地产生¶
为了检测你编写好的.h和.cc文件是否正确,我们需要先在本地运行处理一定事例。在runMultiLepPAT_dataRun3_miniAOD.py中传入所需要的原始root文件cms Data Aggregation System ,并且保证你的CMSSW Release版本和Global Tag与你传入的原始root文件是一致的,运行
如果你运行之后出现了crash的报错,那可能是你的程序的内部逻辑出现了问题,而不是语法错误,这在编译的时候是查不出来的。
如果你的cmsRun可以成功运行,你会发现本地处理event的速度非常慢,三天三夜大概只能处理五万左右的事例,这是因为一个event中包括的track数量是非常庞大的。显然本地处理原始root行不通,因此你需要交到服务器上,让服务器帮助你处理。
2.2-submit crab jobs¶
这在Multilep learning note中的pre 1-CRAB jobs submit已经讲的非常详细了。
在我们提交crab jobs之后,可能需要等待一两天才能跑完所有的数据,但是你不能等它完全finish才开始下一步,一旦有multilep.root产生就立刻开始下一步myntuple分析,这样可以检查你的Ntuple Maker是否仍然存在其他错误,以节省时间,提高效率。
3-myntuple分析root文件¶
3.1-本地运行¶
一个ntuple的job需要myntuple.C.rootmap,myntuple.C,myntuple.h和一个运行的Runjobs.C文件。详细的介绍可以参见Multilep learning note中的5-myntuple分析root文件。这里仅列出我的myntuple.C作为参考。
请记住写好myntuple.C之后,需要进行编译,否则你运行结束产生的图就和上次一模一样。
编译完成之后运行
刚开始你产生的候选事例还比较少,看到的图可能长成下面这个样子。这个时候其实是看不出来到底是否存在信号的,需要用更多的multilep.root。
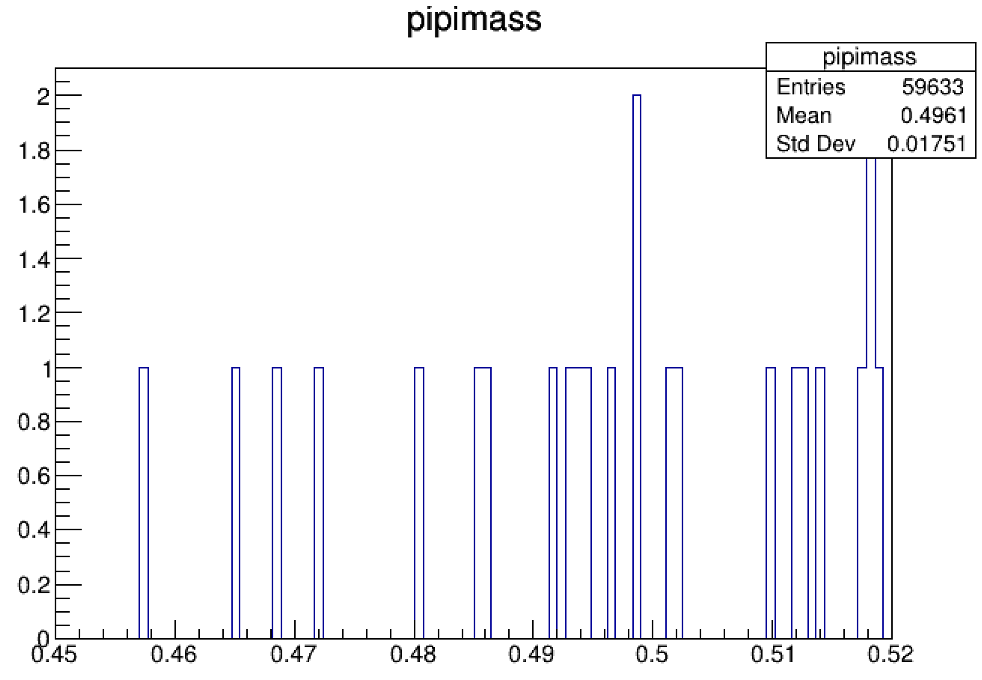
但是在本地myntuple处理数据的过程中,你会发现跑的很慢,大概一万个事例要跑半个小时,效率非常低,因为一个事例的track数目非常庞大。因此需要交condor作业用服务器来帮助你跑。
3.2-submit condor jobs¶
详细的介绍可以参见Multilep learning note中的pre2-Condor Jobs submit。
4-Where is the \(K_s\)¶
当你拥有了足够多的事例之后,你可能会看到下面左侧这样的图,但是你会感觉左侧图的bin分的太细了,有点看不清楚是不是有信号,这里有一个小trick
将bin的数量砍成原来的一半,可以得到右侧的图。
我们发现在0.5GeV左右的地方好像是存在 \(K_s\),但是还不能完全确定。
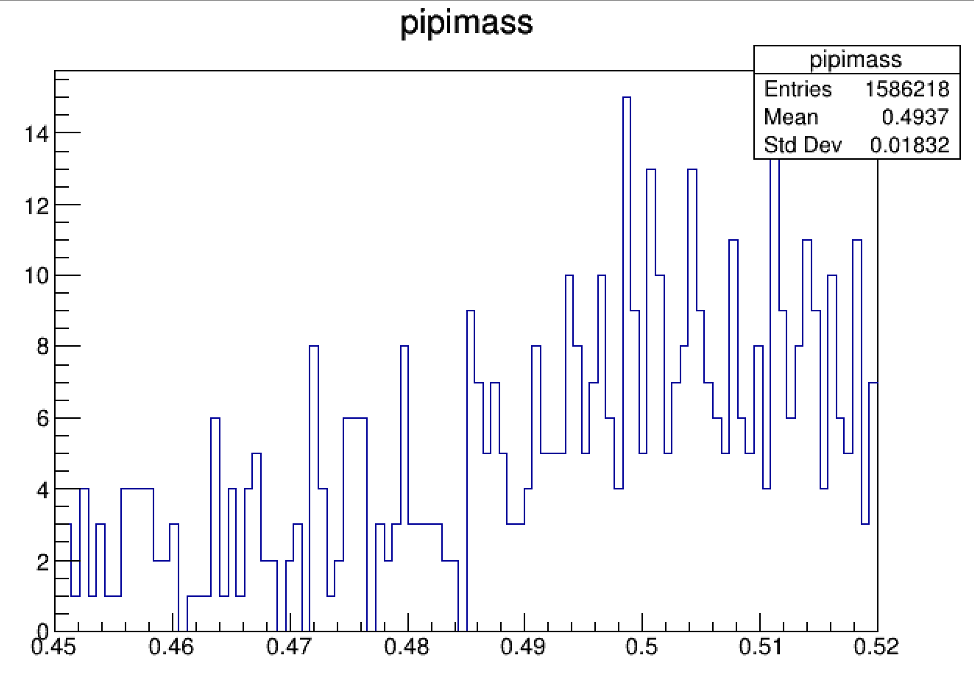
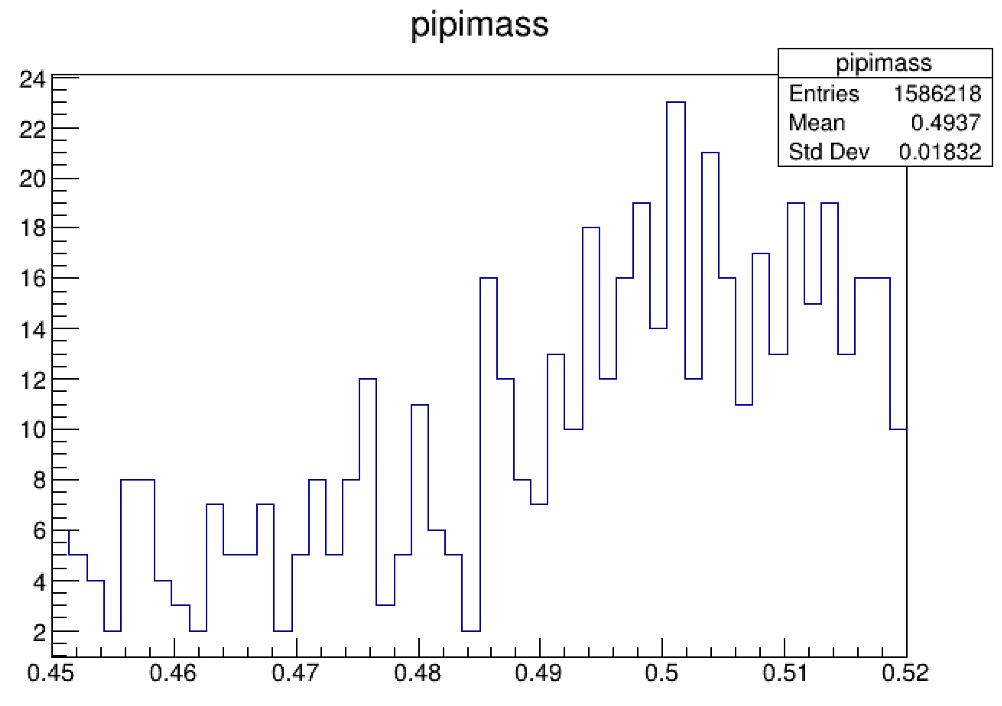
那到底怎么才能看到非常确定的 \(K_s\)呢?
注意到我们在myntuple.C里设置的筛选条件是
可以把条件设的稍微宽松一些
再加之交更多的crab作业,产生更多的multilep.root,我们最终可以得到下面的图
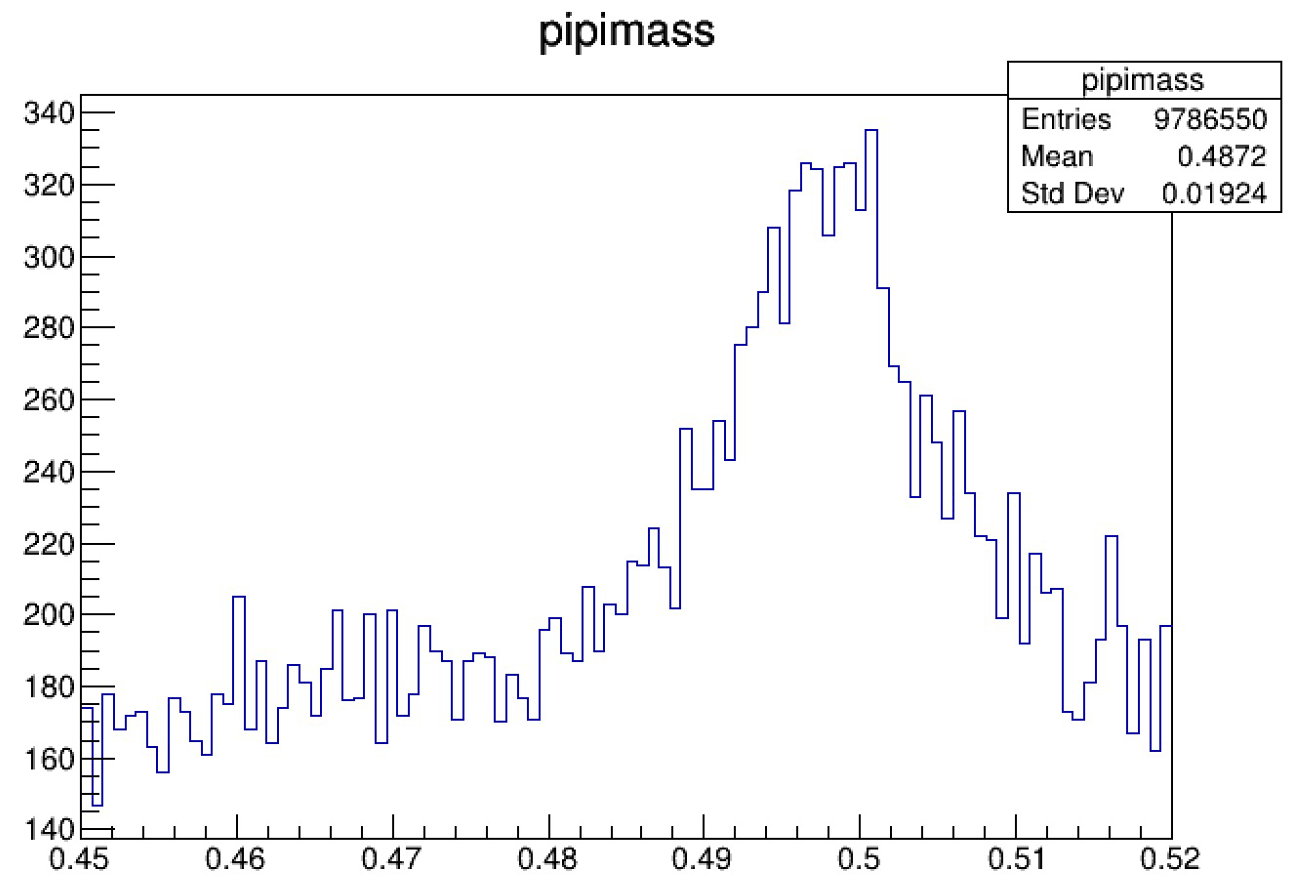
多么pretty的峰!这下我们心里终于有底了,这确确实实就是我们要找的 \(K_s\)!
5-Fit¶
当然,找到信号可以说是已经成功了,但是这还没完,下面我们要对信号进行拟合,看看它的质量、宽度、显著度。
易老师:做事就要把它做完整才算成功。
5.1-直接用直方图拟合¶
拟合的教程在这里可以找到。由于 \(K_s\)的宽度很窄,所以我们采用高斯函数拟合信号,一阶切比雪夫多项式拟合本底。下面仅列出我的fitKs.C作为参考。
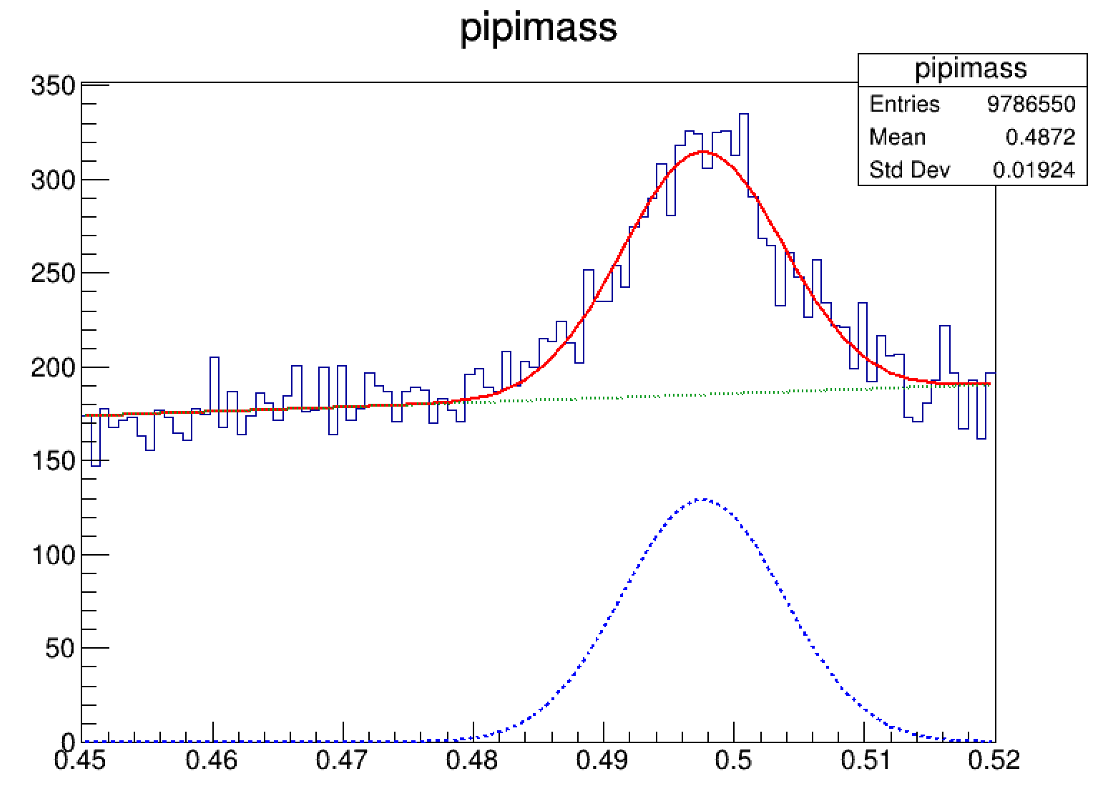
拟合结果是
看到Mean值,已经没有任何人敢质疑你的 \(K_s\)了。而Sigma和我们看到的信号“宽度”是有关的,这里的“宽度”大概是 \(15MeV\),但是我们在PDG上却发现 \(\tau_{K_s}\approx0.8954\times10^{−10}s\),对应的实际宽度 \(\Gamma_{K_s}\approx7.35\times10^{−12}MeV\),这与我们看到的“宽度”相比少了将近12个数量级,因此我们看到的“宽度”其实不是信号真正的宽度,完全是由探测器的resolution(分辨率) 决定的。
5.2-用RooFit拟合¶
在上面的拟合中峰的位置其实并没有处在正中间,感觉不太美观,峰的右侧长啥样也还不知道,我们想把 \(\pi^+\pi^-\)的质量设置在 \([0.45, 0.55]GeV\)之间,但是直方图根本没有把 \(0.52GeV\)以上的数据信息囊括进来。所以我们在实际处理的过程中,一般都会在myntuple.C把信息输出到txt文件里,设置的范围较宽松,然后再在做拟合的时候进一步限制变量范围,这样可以方便随时修改取用。
除此之外,我们还想知道这个信号的Significance是多少,这个可以通过做RooFit拟合计算出来。
RooFit拟合在这里可以找到案例。下面仅列出我的fitKs.C作为参考,我采用的是Unbinned fit。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 | |
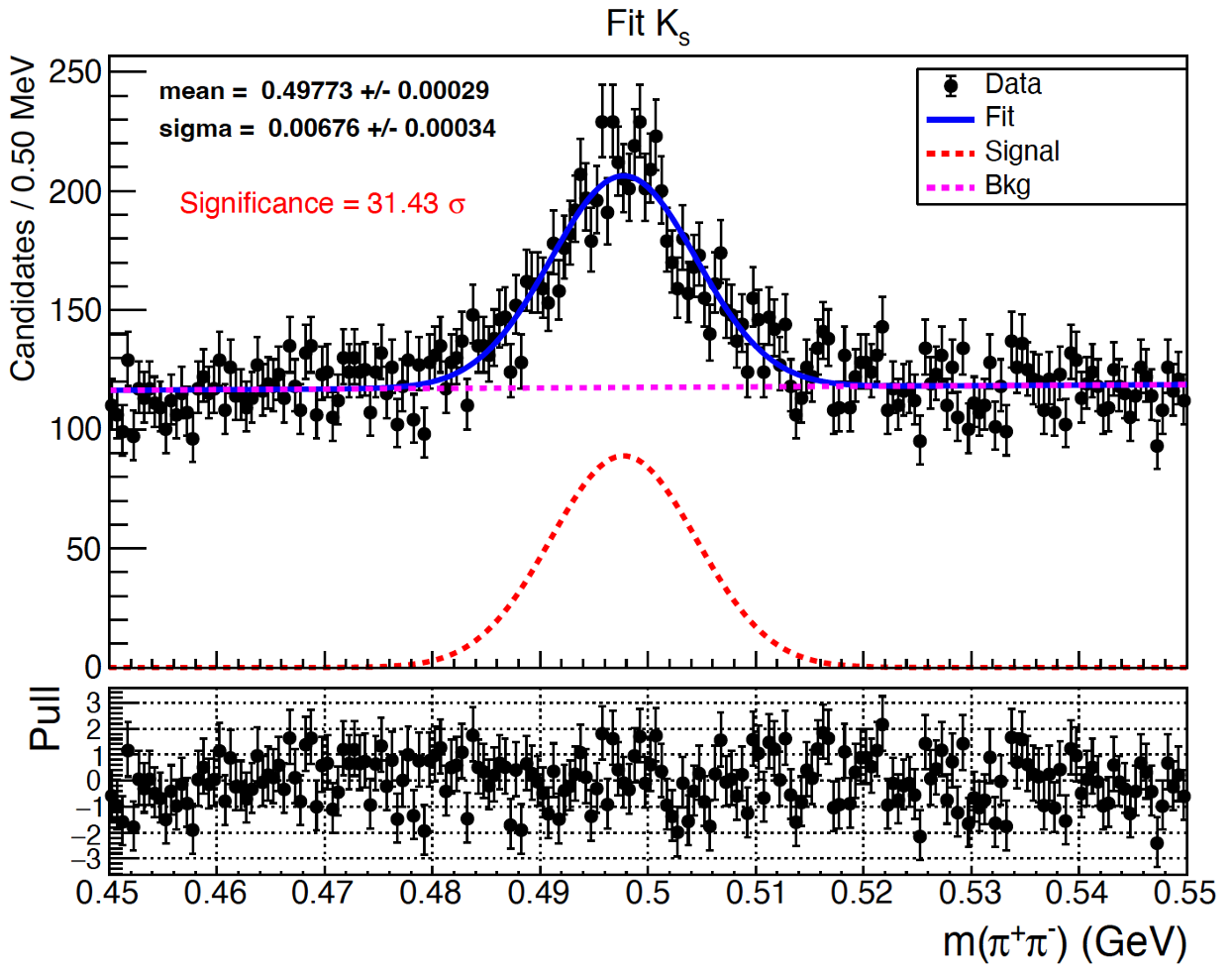
拟合结果已经部分地标在图上了,一个professional的图必须包括Title、X-axis title、Y-axis title、legend、pull分布,所有字体、颜色要合适。
恭喜你!到这儿就已经成功地完整地打通了 \(K_s\)这一关!有没有觉得信心大增?在下一章我们会继续挑战重建 \(\Lambda\)粒子!